What do you call a prediction model that performs tremendously well on the same data it was trained on? Technically, a tosh! It will perform feebly on unseen data, thus leading to a state called overfitting.
To combat such a scenario, the dataset is split into train set and test set. The model is then trained on the train set and is kept deprived of the test set. This test set is utilized to estimate the efficacy of the model. To decide on the best train-test split, two competing cornerstones need to be focused on. Firstly, less training data will give rise to greater variance in the parameter estimates, and secondly, less testing data will lead to greater variance in the performance statistic. Conventionally, an 80/20 split is considered to be a suitable starting point such that neither variance is too high.
Yet another problem arises when we try to fine-tune the hyperparameters. There is a possibility for the model to still overfit on the testing data due to data leakage. To prevent this, a dataset should typically be divided into train, validation, and test sets. The validation set acts as an intermediary between the training part and the final evaluation part. However, this indeed reduces the training examples, thus making it less likely for the model to generalize, and the performance rather depends merely on a random split.
Here’s where cross-validation comes to our rescue!
Cross-validation (CV) eliminates the explicit requirement of a validation set. It facilitates the model selection and aids in gauging the generalizing capability of a model. The rudimentary modus operandi is the k-fold CV, where the dataset is split into k groups/folds and k-1 folds are used to train the model, while the held out kth fold is used to validate the model. Henceforth, each fold gets an opportunity to be used as a test set. This way, in each fold, the evaluation score is retained and the model is then discarded. The model’s skill is summarised by the mean of the evaluation scores. The variance of the evaluated scores is often expressed in terms of standard deviation.
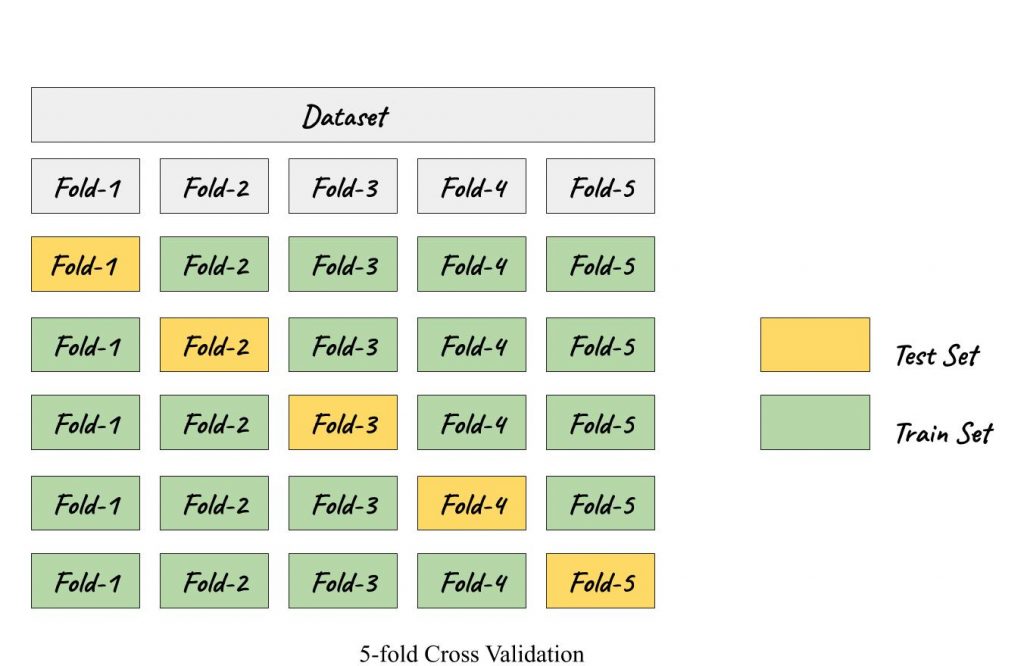
But is it feasible when the dataset is imbalanced?
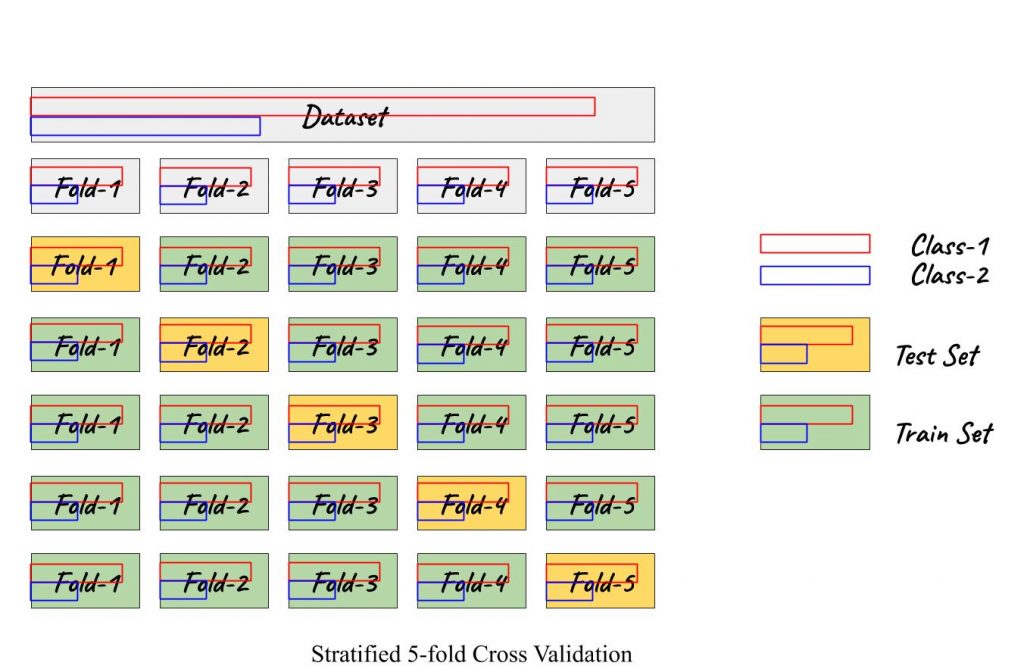
Probably not! In case of imbalanced data an extension to k-fold CV, called Stratified k-fold CV proves to be the magic bullet. It maintains the class proportion in all the folds as it was in the original dataset, thus making it available for the model to train on both, the minority as well as majority classes.
Determining the value of k
This is a baffling concern though! Taking into account the bias-variance trade-off, the value of k should be decided carefully. Consequently, the k value should be chosen such that each fold can act as a representative of the dataset. Jumping on the bandwagon, it is preferred to set the k value as 5 or 10 since experimental success is observed with these values.
There are some other variations of cross-validation viz.,
- Leave One Out CV (LOOCV): Only one sample is held out for the validation part
- Leave P Out CV (LPOCV): Similar to LOOCV, P samples are held out for the validation part
- Nested CV: Each fold involves cross-validation, making it a double cross-validation. It is generally used when tuning hyperparameters
Finally yet importantly, some tidbits that shouldn’t be ignored:
- It is important to shuffle the data before moving ahead with cross-validation
- To avoid data leakage, any data preparation step should be carried out on the training data within the cross-validation loop
- It is preferable to repeat the cross-validation procedure by using repeated k-fold or repeated stratified k-fold CV for more reliable results especially, the variance in the performance metrics.
Voila! We finally made it! If the model evaluation scores are acceptably high and have low variance, it’s time to party hard! Our mojo has worked!
Further Readings:
Knowledge thats worth delivered in your inbox





